問題
5人を3つの部屋 \(A\), \(B\), \(C\) に入れる方法は何通りあるか。ただし, 各部屋には少なくとも1人は入るものとする。
注目ポイント!
"少なくとも"という条件
解答への第一歩
条件での順列(組合せ)を先に考える
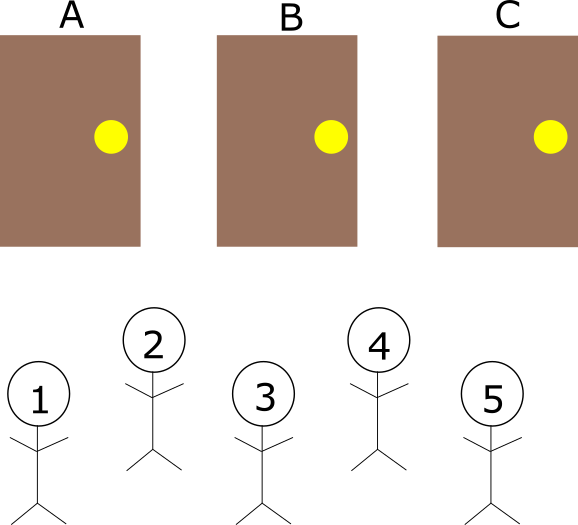
解説
この問題では, 上の絵のような状態のとき, 次の条件を満たすように, 部屋を割り振りする必要がある。
条件:各部屋に少なくとも一人は入るようにする。
そのため先に一人ずつ部屋に割り振ると考えやすくなる。
\(\begin{equation}
\left.
\begin{array}{l}
A:{}_5C_1 = 5\ 通り \\
B:{}_4C_1 = 4\ 通り \\
B:{}_3C_1 = 3\ 通り
\end{array}
\right \} {}_5P_3=5・4・3=60(通り)
\end{equation}\)
残った2人が入る部屋は(残った二人は自由に選べるから)
1人目: 3通り(部屋A,B,C,から選ぶ)
2人目: 3通り(部屋A,B,C,から選ぶ)
この2人が選ぶ部屋の組合せは, \(3・3=9\)(通り)
以上より問題の条件に合う方法は, \(60・9=540\)(通り)