新潟県令和2年実施教員採用試験問題(数学科)解答・解説

問題

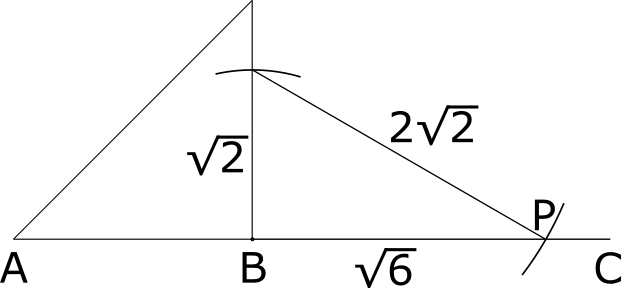
下の図のように, 一直線上に3点 \(A\), \(B\), \(C\) があり, \(AB=2\), \(BC=3\) である。 \(BP=\sqrt{6}\)を満たす点\(P\)の1つを, 定規とコンパスを用いて, 作図によって求め, その点に●をつけなさい。

解説

有名な三角形の比は下の二つの三角形でこれらを活用することを考える。

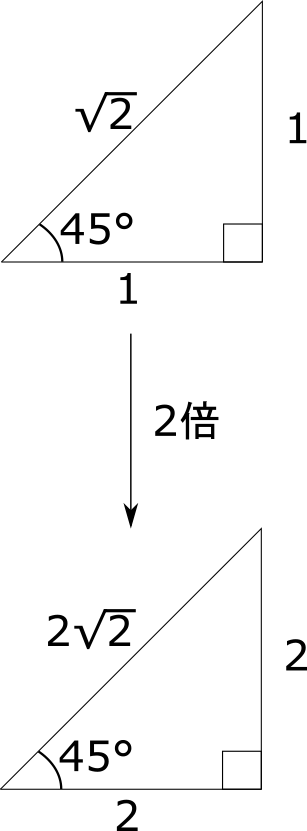
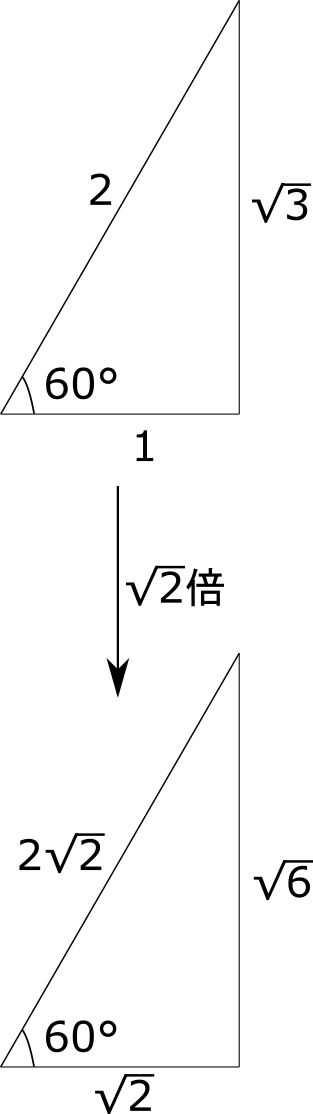
それぞれの三角形を上の図のように拡大すると, \(60^{\circ}\) の三角形の比にて \(\sqrt{6}\) の辺の比が出るため, この三角形を利用する。

他の辺が \(\sqrt{2}\), \(2\sqrt{2}\) である。最初の図の内\(45^{\circ}\)の三角形を点\(B\)が直角で\(AB\)と\(B\)を通る垂線の長さが等しい, 直角二等辺三角形を作図すると下のように描ける。

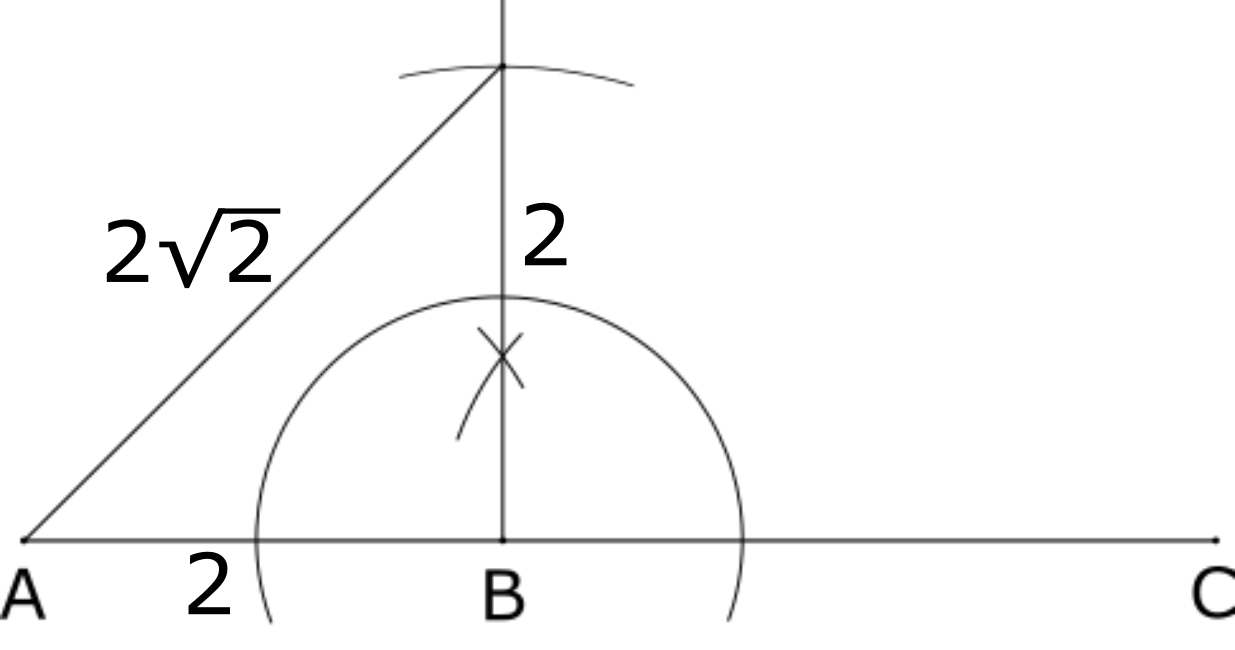
ここで, \(2\sqrt{2}\) の長さが表せた。次に, \(\sqrt{2}\) は \(2\sqrt{2}\) の半分の長さだから, 先ほど書いた三角形の頂点\(B\)の二等分線を描くと下のようになる。

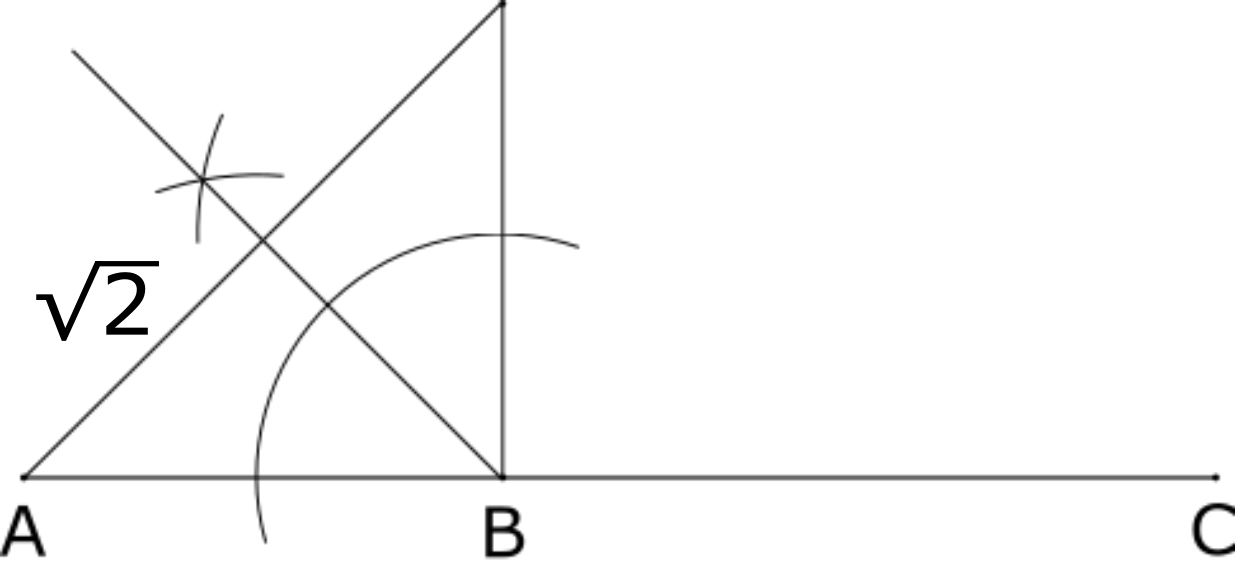
以上で, 今回利用したい \(60^{\circ}\) の三角形の比がすべて表せたので, それぞれの長さをコンパスを利用して, 線分 \(BC\) 側に点 \(P\)を作図すると, 下のように求めることができる。