問題

[3]座標平面上で, 原点 \(O\) で \(x\) 軸に接し, 点 \((0,1)\) を中心とする半径1の円を \(C\) とする。第1象限にある \(C\) 上の点 \(A\) と 原点Oを通る直線と \(x\) 軸の正の向きとのなす角を \(\theta\) とする。 また, \(C\) 上の点\(B\) を, \(C\) の点 \(A\) における法線が \(\angle OAB\) の二等分線となるようにとる。 このとき, 次の(1)～(3)に答えなさい。

(1) \(\triangle\)\(OAB\) は二等辺三角形であることを証明しなさい。

(2) \(\triangle\)\(OAB\) の面積 \(S\) を \(\theta\) を用いて表しなさい。

(3) \(\displaystyle \lim_{\theta \to \frac{\pi}{2}-0} \frac{S}{\frac{\pi}{2}-\theta}\) を求めなさい。

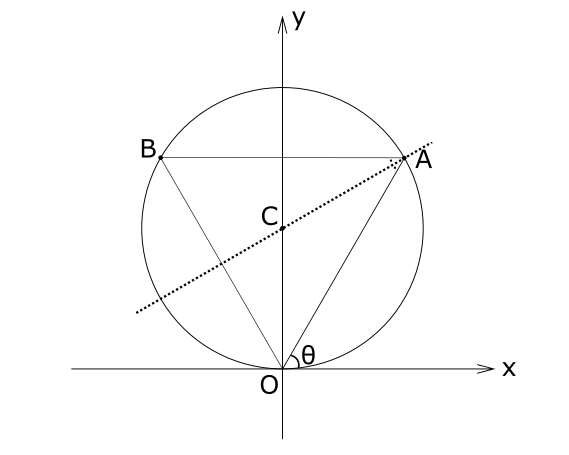
\(\triangle OAB\) において, 頂点 \(B, O\) から, 円の中心Cに補助線を引くと,
\(BC = OC･･･➀\)

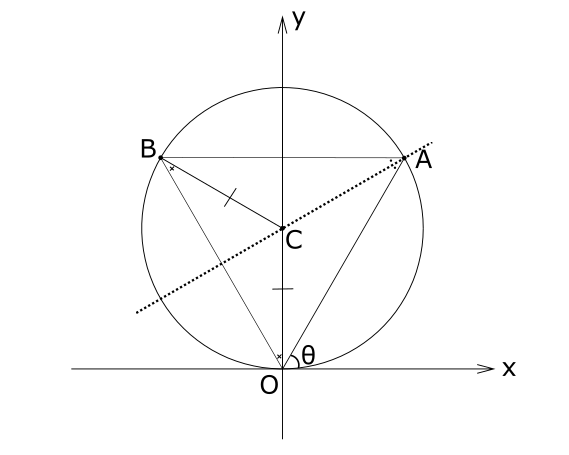
\(➀\)より, \(\angle CBO = \angle COB･･･➀'\)
また, 頂点 \(A\) から円の中心Cに補助線を引くと

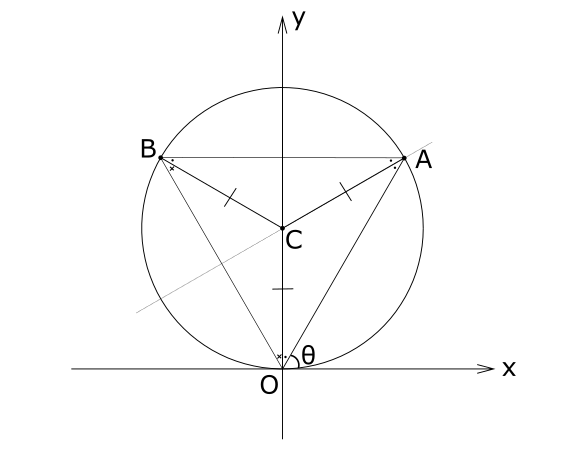
\(\begin{eqnarray} AC &=& BC ･･･➁ \\ AC &=& OC ･･･➂ \end{eqnarray}\)

\(➁\)より \(\angle CAB = \angle CBA ･･･➁'\)
\(➂\)より \(\angle COA = \angle CAO ･･･➂'\)

\(➁',➂'\)より \(\angle CBO + \angle CBA = \angle COB + \angle COA\)
以上より

\(\angle ABO = \angle AOB \)
であるから, \(\angle OAB\) は二等辺三角形である。

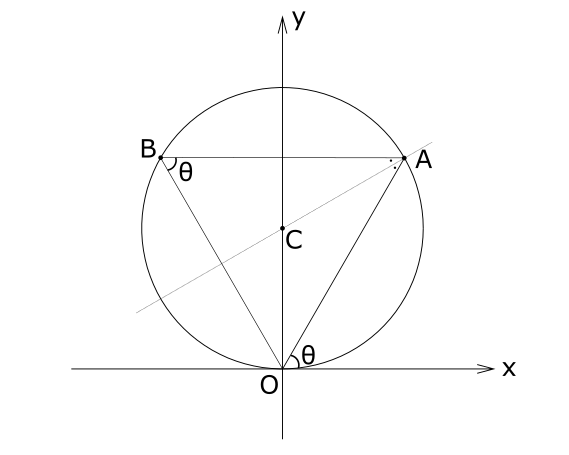
条件より \(\angle ABO = θ\) である。

正弦定理より
\(\begin{eqnarray} AB &=& 2\sin{\theta} \\ BO &=& 2\sin{2\theta} \end{eqnarray}\)

以上より
\(\begin{eqnarray} S &=& \frac{1}{2}AO・BO・\sin{\theta} \\ &=& \frac{1}{2}・2\sin{\theta}・2\sin{2\theta}・\sin{\theta}\\ S &=& 4\sin^3{\theta}\cos{\theta} \end{eqnarray}\)

(2)より, \(S = 4\sin^3{\theta}\cos{\theta}\) である。

ここで,
\(\begin{equation} \left \{ \begin{array}{l} \sin{\theta} &=& \cos{\left(\large \frac{\pi}{2}\normalsize -\theta\right)} \\ \cos{\theta} &=& \sin{\left(\large \frac{\pi}{2}\normalsize -\theta\right)} \\ \end{array} \right. \end{equation}\)
であるから,

\(S = 4\cos^3{\left(\large \frac{\pi}{2}\normalsize -\theta\right)}\sin{\left(\large \frac{\pi}{2}\normalsize -\theta\right)}\)
以上より,
\(\displaystyle \begin{eqnarray} && \lim_{\theta \to \frac{\pi}{2}-0} \frac{4\cos^3{\left(\large \frac{\pi}{2}\normalsize -\theta\right)}\sin{\left(\large \frac{\pi}{2}\normalsize -\theta\right)}}{\large \frac{\pi}{2}\normalsize -\theta} \\ &=& \lim_{\theta \to \frac{\pi}{2}-0} 4\cos^3{\left(\large \frac{\pi}{2}\normalsize -\theta\right)}\frac{\sin{\left(\large \frac{\pi}{2}\normalsize -\theta\right)}}{\large \frac{\pi}{2}\normalsize -\theta} \\ &=& 4\cos^3{0}・1 \\ &=& 4 \end{eqnarray}\)